Persamaan Garis Lurus: Definisi, Grafik, Gradien, dan Menentukan Persamaan Garis Lurus

Sumber: biography.com

 Kita perlu berterima kasih kepada René Descartes. Beliau berperan besar dalam menggabungkan aljabar dan geometri. Berkat beliau, kita sekarang mengenal yang namanya sistem koordinat cartesius. Makanya sekarang kita bisa menggambar suatu persamaan (aljabar) ke dalam suatu grafik pada koordinat kartesius (geometri).

Lalu apa sih persamaan garis lurus? Dari namanya saja sudah jelas bahwa persamaan garis lurus adalah persamaan yang grafiknya berupa garis lurus. Untuk lebih jelasnya, yuk kita bahas bersama.

Persamaan Garis Lurus

Persamaan garis lurus (PGL) adalah persamaan yang grafiknya berupa garis lurus. Persamaan garis lurus termasuk persamaan linear.

Bentuk umum:

ax + by + c = 0

dengan x dan y adalah variabel, a adalah koefisien dari x, b adalah koefisien dari y, c adalah konstanta. Pangkat variabelnya adalah satu. Penyelesaian dari persamaan garis lurus adalah pasangan-pasangan terurut (x, y) yang memenuhi persamaan tersebut. Apabila pasangan-pasangan terurut tersebut digambarkan pada bidang koordinat cartesius (koordinat-xy), akan didapatkan suatu garis lurus.

Grafik Persamaan Garis Lurus

Persamaan garis lurus dapat digambarkan dalam koordinat cartesius. Berikut langkah-langkah dalam menggambar grafik PGL.

Langkah 1

Tentukan koordinat dua titik yang dilalui oleh garis (grafik persamaan garis lurus). Titik yang dilalui oleh grafik persamaan garis lurus adalah pasangan-pasangan terurut (x, y) yang memenuhi persamaan tersebut. Untuk memudahkan, cari saja titik potong garis terhadap sumbu x dan sumbu y. Titik potong terhadap sumbu x diperoleh ketika y = 0 dan titik potong terhadap sumbu y diperoleh ketika x = 0.

Langkah 2

Tempatkan kedua titik tersebut pada koordinat cartesius.

Langkah 3

Hubungkan kedua titik tersebut dengan garis lurus dan voila! jadilah grafik persamaan garis lurus.

Contoh

Gambarkan grafik y = 4 - 6x!

Langkah 1

    Titik potong terhadap sumbu x (y = 0)

    y = 4 - 6x ⇒ 0 = 4 - 6x 

                    ⇔ 6x = 4

                    ⇔ x = 4/6

                    ⇔ x = 2/3

    diperoleh titik potong terhadap sumbu x adalah (2/3, 0)

    Titik potong terhadap sumbu y (x = 0)

    y = 4 - 6x ⇒ y = 4 - 6(0) 

                    ⇔ y = 4

    diperoleh titik potong terhadap sumbu y adalah (0, 4)

Langkah 2

Tempatkan titik (2/3, 0) dan (0,4) pada koordinat cartesius

Langkah 3

Hubungkan titik (2/3, 0) dan (0,4) dengan garis lurus. 

Jadilah grafik persamaan garis lurus y = 4 - 6x.

Gradien Garis Lurus

Gradien adalah nilai yang menunjukkan kemiringan atau kecondongan suatu garis lurus. Gradien biasanya dinotasikan dengan huruf "m". Gradien menentukan seberapa miring suatu garis pada koordinat kartesius. Gradien suatu garis dapat miring ke kanan, miring ke kiri, curam, ataupun landai, tergantung dari nilai komponen x dan komponen y nya. Garis yang bergradien positif akan miring ke kanan, sedangkan garis yang bergradien negatif akan miring ke kiri. 

Untuk menentukan nilai gradien dari garis lurus, terdapat dua kasus.

Kasus I (jika diketahui persamaan garis lurusnya)

Misalkan terdapat suatu persamaan garis lurus 

y = mx + n

dengan x dan y adalah variabel, dan n adalah konstanta, maka m adalah gradien dari garis lurus tersebut.

Apabila persamaan garis lurus berbentuk ax + by + c = 0, maka kita ubah terlebih dahulu menjadi y = ... 

sehingga diperoleh gradiennya adalah -a/b.

Contoh

Tentukan gradien dari:

a. y = -2x - 15

b. 3y = 6x -12

c. 4y - 5x = 7

d. (1/2)x -10y = 20

e. 2y + 8x + 16 = 0

f. 3y = 0

g. x = 4

Pembahasan
a. y = -2x - 15 maka gradiennya adalah -2.

b. 3y = 6x -12 ⇔ y = 2x - 4, maka gradiennya adalah 2.

c. 4y - 5x = 7 ⇔ 4y = 5x + 7

                       ⇔ y = (5/4)x + (7/4)

    maka gradiennya adalah 5/4.

d. (1/2)x -10y = 20 ⇔ -10y = -(1/2)x + 20

                                ⇔      y = (1/20)x - 2

    maka gradiennya adalah 1/20.

e. 2y + 8x + 16 = 0 ⇔ 2y = -8x - 16

                               ⇔   y = -4x - 8

    maka gradiennya adalah -4.

f. 3y = 0 ⇔ y = 0, maka gradiennya adalah 0.

g. x = 4, maka gradiennya adalah ∞ (karena grafiknya tidak miring)

Kasus II (jika diketahui dua yang dilalui garis)

Misalkan terdapat garis lurus yang melalui titik (x1,y1) dan (x2,y2), maka gradien garisnya dapat diperoleh dengan

Contoh

Tentukan gradien dari garis berikut.

Pembahasan

Garis tersebut melalui titik (2/3, 0) dan (0,4). Misalkan  (x1,y1) = (2/3, 0) dan (x2,y2) = (0,4), maka gradiennya adalah m = (y2 - y1)/(x2- x1) = (4-0)/(0-2/3) = 4/(-2/3) = -6.

Hubungan Dua Garis Lurus Berdasarkan Gradien

Misalkan terdapat dua garis dengan persamaan berturut-turut y = m1 x + n1 dan y = m2 x + n2.

(i) Jika dua garis tersebut saling sejajar, maka gradien kedua garis tersebut sama (m1 = m2).

(i) Jika dua garis tersebut saling tegak lurus, maka hasil kali dari gradien kedua garis tersebut adalah -1 (m1.m2 = -1), sehingga m1 = -1/m2 atau m2  = -1/m1.

Menentukan Persamaan Garis Lurus

Terdapat dua kasus saat mencari suatu persamaan garis lurus, yaitu:

Kasus I (Jika diketahui gradien dan satu titik yang dilalui garis)

Misalkan terdapat suatu garis y = mx + n yang  bergradien m dan melalui titik (x1,y1).

Apabila kita substitusikan titik (x1,y1) ke dalam persamaan garis, akan diperoleh

y1 = mx1 + n 

Sehingga

              y = mx + n

             y1 = mx1 + n

            --------------- -

     (y - y1) = mx - mx1

⇔  (y - y1) = m(x - x1)

Jadi persamaan gar dapat ditentukan dengan

(y - y1) = m (x - x1)

Kasus II (Jika diketahui dua titik yang dilalui garis)

Misalkan terdapat garis yang melalui titik (x1,y1) dan titik (x2,y2). Persamaan garis yang melalui titik (x1,y1) dengan memisalkan gradiennya m adalah 

(y - y1) = m(x - x1) ... (i)

Gradien dari garis tersebut adalah m = (y2 - y1)/(x2- x1) ... (ii)

Dengan mensubstitusi (ii) ke (i), akan diperoleh

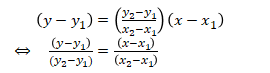
Jadi persamaan garis lurus dapat ditentukan dengan

Contoh

1. Tentukan persamaan garis k yang memotong sumbu y = 5 dan tegak lurus dengan garis p yang melalui titik pusat O dan titik (5, 4).

Pembahasan

Diketahui: 

• garis k memotong sumbu y = 5
• garis p melalui titik (0,0) dan titik (5, 4)
• garis k ⊥ garis p maka mk.mp = -1

Kita cari dahulu gradien dari garis p

mp = (y2 - y1)/(x2- x1) = (4-0)/(5-0) = 4/5 

mk.mp = -1 ⇒ mk.(4/5) = -1

                  ⇔         mk = -5/4

Garis k memotong y = 5, artinya garis k melalui titik (0,5). 

(y - yk) = mk (x - yk)  ⇒          (y - 5) = -5/4 (x - 0)  

                                  ⇔             y - 5 = (-5/4)x

                                  ⇔         4y - 20 = -5x

                                  ⇔ 5x + 4y - 20 = 0

Jadi persamaan garis k adalah 5x + 4y - 20 = 0

2. Suatu garis q yang melalui titik (-2, 2) dan (8, s) sejajar dengan garis 5y + 3x = -9. Tentukan nilai s!

Pembahasan

Diketahui: 

• melalui titik (-2, 2) dan (8, s)
• sejajar dengan 5y + 3x = -9 

Gradie garis q

mq = (y2 - y1)/(x2- x1) = (s-2)/(8-(-2)) = (s-2)/10

5y + 3x = -9 ⇔ 5y = -3x - 9

                     ⇔   y = (-3/5)x - (9/5)

maka gradien garis 5y + 3x = -9 adalah -3/5

Karena sejajar dengan garis 5y + 3x = -9, maka gradien garis q sama dengan garis 5y + 3x = -9.

mq = (s-2)/10 = -3/5

    ⇔    5(s-2) = -3(10)

    ⇔   5s - 10 = -30

    ⇔           5s = -20

    ⇔            s = -4

-------‐-----------------

Kira-kira begitulah mengenai persamaan linear dua variabel atau persamaan garis lurus. Semoga artikel ini bermanfaat. Kalau ada yang keliru, tolong dikasih tau yaa.. biar kita sama-sama belajar.

Selamat Belajar~

Salam Ngemeal 🥘