Fungsi Linear: Definisi, Grafik, dan Contoh Soal Beserta Pembahasannya

Masih ingat materi tentang fungsi, kan? Hayooo inget-inget lagi apa yang dimaksud dengan fungsi? Betul, fungsi adalah relasi dari himpunan A ke himpunan B dengan setiap anggota himpunan A berpasangan dengan tepat satu anggota himpunan B. Dan ingat! himpunan A dan himpunan B tidak kosong. Kalau masih lupa, bisa liat dulu artikel mengenai fungsi. 

Seperti yang kita ketahui, fungsi itu bermacam-macam. Ada fungsi linear, fungsi kuadrat, fungsi polinom, fungsi eksponen, fungsi logaritma, dan masih banyak lagi. Pada artikel ini, akan dibahas mengenai fungsi linear. 

Apa yang terlintas pada benak kalian ketika mendengar kata linear? *mikirkeras*. Menurut Kamus Besar Bahasa Indonesia, linear artinya berbentuk garis. Hmmm... berarti fungsi linear itu fungsi yang berbentuk garis? Yaaa!! lebih tepatnya grafik fungsinya yang berbentuk garis lurus. Agar lebih jelas, mari kita jabarkan.

Definisi Fungsi Linear

Fungsi linear merupakan fungsi yang pangkat tertinggi dari variabelnya adalah satu, atau bisa juga disebut fungsi berderajat satu atau berordo satu. Fungsi linear termasuk fungsi polinom atau fungsi suku banyak.

Bentuk umum

Misalkan terdapat fungsi f: x ➝ mx + b atau dapat dituliskan

f(x) = mx + b ⇔ y = mx + b

dengan m, b ∈ R, x adalah variabel bebas (variabel yang menjelaskan variabel terikat), y atau f(x) adalah variabel terikat (variabel yang dijelaskan oleh variabel bebas), m adalah koefisien dari x, dan b adalah konstanta. 

Daerah asal (domain) fungsi linear adalah semua bilangan real x, ditulis Df = {x| x ∈ R} atau Df = x ∈ (-∞, ∞), sehingga daerah hasil (range) nya pun adalah semua bilangan real y, ditulis Rf = {y| y ∈ R} atau Rf = y ∈ (-∞, ∞). Apabila daerah asal (domain) fungsi linear sudah ditetapkan atau dicantumkan secara eksplisit, untuk menentukan daerah hasilnya bisa dibaca disini.

Karena fungsi linear dapat dinyatakan menjadi persamaan linear, grafik fungsi linear sama seperti grafik dari persamaan linear di ruang dimensi dua atau persamaan garis lurus. Nilai m merupakan gradien atau kemiringan atau kecondongan atau kecuraman atau koefisien arah, dan b adalah titik potong (titik penggal) grafik dengan sumbu y. Gradien menentukan seberapa miring suatu garis (grafik fungsi linear) pada koordinat kartesius. Grafik fungsi linear yang bergradien positif akan miring ke kanan, sedangkan grafik fungsi linear yang bergradien negatif akan miring ke kiri. 

Grafik Fungsi Linear

Menggambar Grafik Fungsi Linear

Sebelumnya sudah dibahas bahwa fungsi linear memiliki grafik berupa garis lurus. Untuk menggambar grafik, terdapat dua metode, yaitu metode mendaftar dan metode matematis.

Metode Mendaftar

Metode ini dilakukan dengan cara mendaftarkan nilai variabel bebas (misalnya x) untuk mendapatkan nilai fungsinya (misalnya f(x)) sehingga diperoleh pasangan terurut (x, f(x)) yang merupakan titik koordinat, biasanya disajikan dalam bentuk tabel. Kemudian letakkan titik koordinatnya pada koordinat cartesius dan hubungkan titik-titik koordinat tersebut dengan garis lurus.

Metode Matematis

Metode ini dilakukan dengan mencari ciri-ciri matematis dari grafik fungsi. Pada fungsi linear, kita dapat menggambar grafik fungsinya hanya dengan dua titik yang dilalui oleh grafik. Titik yang dilalui oleh grafik fungsi adalah pasangan-pasangan terurut (x, f(x)) atau (x, y) yang memenuhi fungsi tersebut. Untuk memudahkan, cari saja titik potong grafik terhadap sumbu x (x1, 0) dan sumbu y (0, y1). Titik potong terhadap sumbu x diperoleh ketika y = 0 dan titik potong terhadap sumbu y diperoleh ketika x = 0. Kemudian tempatkan kedua titik potong tersebut pada koordinat cartesius dan hubungkan kedua titik tersebut dengan garis lurus.

Note: Kalau menurut saya pribadi, menggambar grafik fungsi linear lebih mudah dengan mencari titik potong grafik terhadap sumbu x dan sumbu y. Karena bentuk grafik fungsi linear adalah garis, dua titik saja sudah cukup untuk menggambar grafiknya.

Contoh

Gambarkan grafik fungsi f dengan f(x) = (1/2)x + 5!

Pembahasan

Metode Mendaftar

Kita pilih beberapa bilangan real yang akan mengganti x. Misalkan pilih -2, 0, 1, 2, 4, 6. Pilih bilangan pecahan juga boleh, pokoknya bilangan apa saja. Saya pilih bilangan bulat untuk mempermudah perhitungan. Kemudian kita tentukan nilai fungsi untuk setiap x yang kita pilih sebelumnya. 

Untuk x = - 2

f(-2) = (1/2)(-2) + 5 = -1 + 5 = 4

diperoleh titik koordinat (-2, 4)

Untuk x = 0

f(0) = (1/2)(0) + 5 = 0 + 5 = 5

diperoleh titik koordinat (0, 5)

Untuk x = 1

f(1) = (1/2)(1) + 5 = 1/2 + 5 = 11/2

diperoleh titik koordinat (1, 11/2)

Untuk x = 2

f(2) = (1/2)(2) + 5 = 1 + 5 = 6

diperoleh titik koordinat (2, 6)

Untuk x = 4

f(4) = (1/2)(4) + 5 = 2 + 5 = 7

diperoleh titik koordinat (4, 7)

atau bisa didaftarkan dalam bentuk tabel

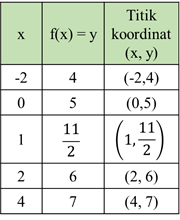
Kemudian kita letakkan titik-titik koordinat pada koordinat kartesius. Setelah itu hubungkan titik-titik koordinat dengan garis lurus, sehingga didapat grafiknya sebagai berikut.

Metode matematis
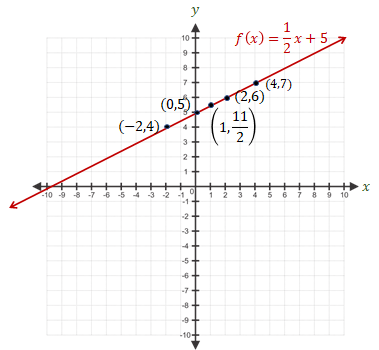
f(x) = (1/2)x + 5 ⇔ y = (1/2)x + 5

maka gradiennya adalah 1/2. Karena gradiennya positif, maka grafik fungsi akan miring ke kanan.

Titik potong terhadap sumbu x (syarat: y = 0)

 y = (1/2)x + 5 ⇒          0 = (1/2)x + 5

                        ⇔ (1/2) x = -5

                        ⇔          x = -10

Diperoleh titik potong terhadap sumbu x nya adalah (-10, 0)

Titik potong terhadap sumbu y (syarat: x = 0)

 y = (1/2)x + 5 ⇒ y = (1/2)(0) + 5

                                = 0 + 5

                                = 5

Diperoleh titik potong terhadap sumbu y nya adalah (0, 5)

Kemudian kita letakkan titik-titik potong pada koordinat kartesius. Setelah itu hubungkan titik-titik tersebut dengan garis lurus, sehingga didapat grafiknya sebagai berikut.

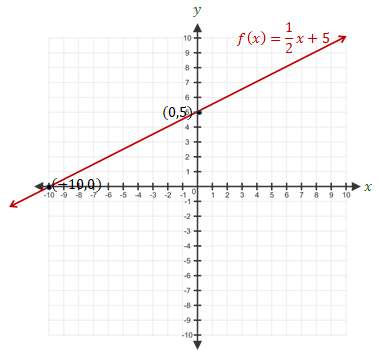
Gradien Grafik Fungsi Linear

Gradien atau koefisien arah adalah nilai yang menunjukkan kemiringan atau kecondongan suatu garis lurus. Gradien biasanya dinotasikan dengan huruf "m". Gradien menentukan seberapa miring suatu garis pada koordinat kartesius. Suatu garis dapat miring ke kanan, miring ke kiri, curam, ataupun landai, tergantung dari nilai komponen x dan komponen y nya. Garis yang bergradien positif akan miring ke kanan, sedangkan garis yang bergradien negatif akan miring ke kiri. 

Perhatikan gambar berikut.

Misalkan terdapat fungsi linear f dengan f(x) = mx + b, dengan m, b ∈ R, maka m adalah gradien dari grafik fungsi tersebut. Jika m > 0 (m bernilai positif), maka grafik fungsi linear akan miring ke kanan. Jika m < 0 (m bernilai negatif), maka grafik fungsi linear akan miring ke kiri. 

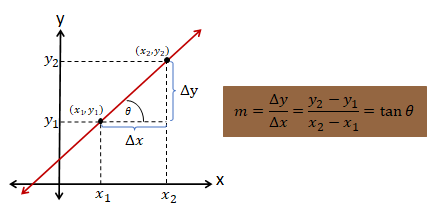
Menentukan Rumus Fungsi Linear 

Karena grafik fungsi linear berupa garis lurus, maka untuk menentukan rumus suatu fungsi linear sama seperti mencari persamaan garis lurus.

Jika grafik fungsi linear melalui satu titik dan bergradien m

Misalkan terdapat fungsi linear f dengan f(x) = mx + b yang melalui titik (x1,y1) dan bergradien m. 

f(x) = mx + b ⇔ y = mx + b ... (i)

Apabila kita substitusikan titik ke dalam fungsi, akan diperoleh

f(x1) = mx1 + b ⇔ y1 = mx1 + b ...(ii)

Dari (i) dan (ii), akan diperoleh

              y = mx + b

             y1 = mx1 + b

            --------------- -

     (y - y1) = mx - mx1

⇔  (y - y1) = m(x - x1)

Jadi rumus fungsi linear dapat ditentukan dengan

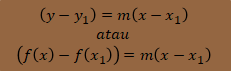
Jika grafik fungsi linear melalui dua titik

Misalkan terdapat fungsi linear f yang melalui titik (x1,y1) dan titik (x2,y2). Persamaan garis (grafik fungsi linear) yang melalui titik (x1,y1) dengan memisalkan gradiennya m adalah 

(y - y1) = m(x - x1) ... (i)

Gradien dari grafik fungsi linear f adalah m = (y2 - y1)/(x2- x1) ... (ii)

Dengan mensubstitusi (ii) ke (i), akan diperoleh

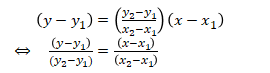
Jadi rumus fungsi linear dapat ditentukan dengan

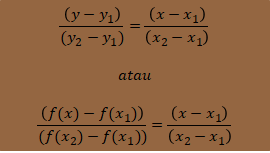
Soal Latihan

1. Diketahui g(x) = 4 - 5x. Jika g(2) = a dan g(b) = -11, tentukan nilai 2a² + b!

2. Diketahui h(x) = ax + b. Jika h(3) = 8 dan h(-2) = -17, tentukan rumus fungsi h!

3. Gambarkan grafik fungsi s(x) = 6 - 3x!

4. Tentukan rumus fungsi f apabila grafiknya sebagai berikut.

Pembahasan

1. Diketahui:

• g(x) = 4 - 5x
• g(2) = a
• g(b) = -11

    g(2) = 4 - 5(2) = a

          ⇔   4 - 10 = a

          ⇔           a = -6

    

    g(b) = 4 - 5b = - 11

          ⇔   - 5b = -15

          ⇔        b = 3

    Diperoleh a = -6 dan b = 3.

    2a² + b = 2(-6)² + 3 = 2(36) + 3 = 75

2. Diketahui:

• h(x) = ax + b
• h(3) = 8 
• h(-2) = -17

    h(3) = a(3) + b = 8

           ⇔  3a + b = 8 ...(i)

    

    h(-2) = a(-2) + b = - 17

            ⇔   -2a + b = -17 ... (ii)

    Dari (i) dan (ii)

    3a + b = 8

   -2a + b = -17

    --------------- -

    5a       = 25

⇔  a       = 5

    Substitusi a = 5 ke (i)

    3(5) + b = 8 ⇔ 15 + b = 8

                        ⇔         b = -7

    Diperoleh a = 5 dan b = -7, sehingga rumus fungsi h adalah h(x) = 5x - 7.

3. s(x) = 6 - 3x ⇔ y = 6 - 3x maka gradiennya adalah -3. Karena gradiennya negatif, maka grafik fungsi akan miring ke kiri.

Titik potong terhadap sumbu x (syarat: y = 0)

 y = 6 - 3x ⇒   0 = 6 - 3x

                 ⇔ 3x = 6

                 ⇔   x = 2

Diperoleh titik potong terhadap sumbu x nya adalah (2,0)

Titik potong terhadap sumbu y (syarat: x = 0)

 y = 6 - 3x ⇒   y = 6 - 3(0)

                           = 6

Diperoleh titik potong terhadap sumbu y nya adalah (0, 6)

Grafik fungsi s sebagai berikut.

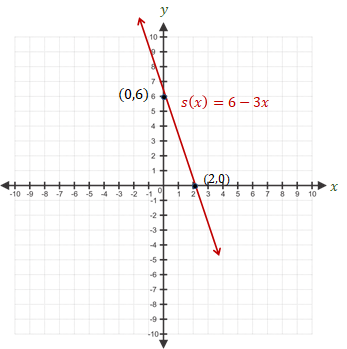
4. 

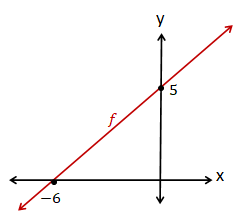
Dari gambar grafik f, kita peroleh bahwa grafik f melalui titik (-6,0) dan (0,5), sehingga rumus fungsi f dapat diperoleh dengan 

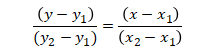
Misalkan titik (x1,y1) adalah (-6,0) dan titik (x2,y2) adalah (0,5), maka

Jadi rumus fungsi linear f adalah f(x) = (5/6)x + 5

--------------------------------------

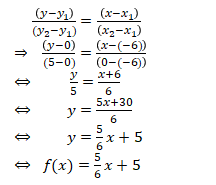
Fungsi linear memang berkaitan dengan persamaan linear di ruang berdimensi dua atau persamaan garis lurus, karena fungsi linear dapat dinyatakan menjadi persamaan linear [f(x) = ax + b ⇔ y = ax + b] sehingga mempermudah dalam pembuatan grafik fungsinya. Tapi hati-hati!! tidak semua persamaan linear adalah fungsi linear (ex: x = 5). Untuk lebih jelasnya, silakan tengok artikel mengenai persamaan linear. 

Semoga artikel ini dapat bermanfaat. Apabila ada yang keliru, tolong tulis di kolom komentar yaa.. agar kita bisa saling share informasi 😊

Selamat Belajar ~

Salam Ngemeal 🍲