Fungsi (Part I): Relasi, Definisi, Unsur, Jenis Fungsi Beserta Contoh [LENGKAP]

Materi kali ini, akan sering kamu jumpai di materi mendatang. Pokoknya penting banget untuk kamu paham mengenai konsep fungsi. Sebenarnya apa sih fungsi itu? Apakah fungsi yang dimaksud adalah manfaat? Bukan ya kawan. Fungsi di matematika bukanlah berarti manfaat. Sebelum kenalan dengan fungsi, kenalan dulu dengan relasi, yuk.
Relasi
Setiap orang pasti memiliki golongan darah yang berbeda-beda, bukan? Nah, itulah salah satu contoh relasi. Kamu pasti gak asing dengan kata relasi. Yaps, relasi adalah hubungan, misalnya hubungan kamu dengan si dia #cieee. Secara matematis, relasi adalah suatu hubungan antara dua himpunan yang tidak kosong.
Misalkan, keluarga Riko masing-masing memiliki golongan darah yaiyalah punya golongan darah namanya juga manusia.
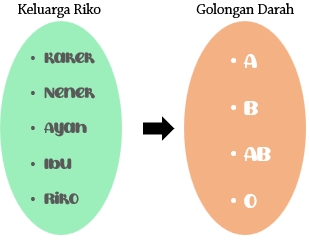



Kakeknya memiliki golongan darah A, neneknya memiliki golongan darah B, ayahnya memiliki golongan darah AB, Ibunya bergolongan darah O, dan Riko bergolongan darah A. Di sini, kita peroleh dua himpunan tak kosong, yaitu himpunan keluarga Riko dan himpunan golongan darah. Lalu apa relasi antara himpunan keluarga Riko dan himpunan golongan darah? Terdapat dua relasi yang terbentuk.
Relasi I (Pemilik golongan darah)

Daerah asal (domain)nya adalah himpunan keluarga Riko, sedangkan daerah hasil atau kodomainnya adalah himpunan golongan darah.
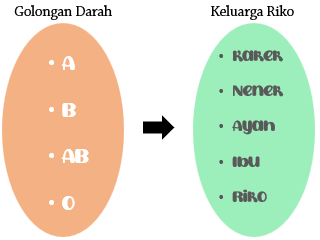
Relasi II (Golongan darah dari)

Daerah asal (domain)nya adalah himpunan golongan darah, sedangkan daerah hasil atau kodomainnya adalah himpunan keluarga Riko.
Relasi dapat dinyatakan dengan tiga cara, yaitu diagram panah, himpunan pasangan terurut, dan diagram Cartesius. Berikut ini adalah pernyataan relasi "pemilik golongan darah" dalam 3 cara tersebut.

Contoh
Diketahui A = {1,2,3,4,5} dan B = {2,4,6,8,12}.
Dari A ke B dihubungkan relasi "setengah dari". Daerah asal (domain) adalah himpunan A. Daerah kawan (kodomain) adalah himpunan B. Daerah hasil (range) adalah {2,4,6,8}. Dua belas tidak termasuk range karena tidak memiliki pasangan.

Dari B ke A dihubungkan relasi "dua kali dari". Daerah asal (domain) adalah himpunan B. Daerah kawan (kodomain) adalah himpunan A. Daerah hasil (range) adalah {1,2,3,4}. Lima tidak termasuk range karena tidak memiliki pasangan.

Fungsi (Pemetaan)
Kamu pasti tahu vending machine atau mesin minuman yang biasanya ada di pinggir beberapa jalan, atau bahkan di mall. Cara kerja mesin tersebut, kita masukan uang ke mesin, lalu diproses, hingga akhirnya minumannya keluar dari mesin. Cara kerja fungsi dalam matematika kurang lebih seperti itu. Misalnya ada fungsi f(x) = x + 4. Kita pilih masukannya x =2. Lalu kita proses f(2) = 2 + 4. Akhirnya diperoleh f(2) = y = 6. Apa bedanya relasi dengan fungsi? Coba tengok dulu definisi fungsi.
Definisi Fungsi (Pemetaan)
Misalkan terdapat A dan B himpunan-himpunan yang tidak kosong. Suatu fungsi f dari A ke B, ditulis f: A ⇾ B (dibaca fungsi f memetakan A ke B), adalah suatu aturan yang memasangkan setiap x ∈ A dengan tepat satu anggota f(x) ∈ B.
Dalam definisi, x dinamakan variabel bebas, sedangkan y dinamakan variabel terikat karena nilainya tergantung dari x. Himpunan A dinamakan daerah asal (domain) fungsi f dan dinotasikan dengan Df = A = {x| x ∈ A}. Himpunan B dinamakan daerah kawan (kodomain) fungsi f dan dinotasikan dengan Kf = B. Himpunan {f(x)| x ∈ A} dinamakan daerah hasil (range) fungsi f dan dinotasikan dengan Rf = {f(x)| x ∈ A}.
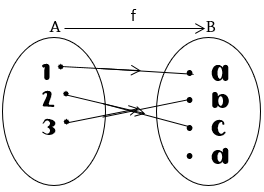
Contoh

Himpunan A = {1,2,3} adalah daerah asal (domain) dari fungsi f. Himpunan B adalah daerah kawan (kodomain) fungsi f. Sedangkan, range dari fungsi f tersebut adalah {a, b, c}.
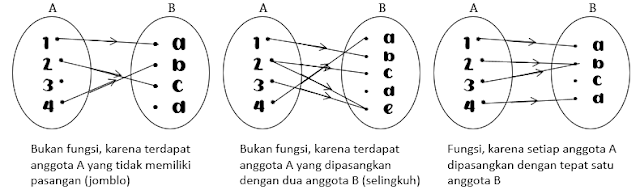
Intinya, fungsi adalah relasi dari himpunan A ke himpunan B dengan setiap anggota himpunan A berpasangan dengan tepat satu anggota himpunan B. Jadi anggota himpunan A-nya ga boleh jomblo dan ga boleh selingkuh.
Contoh
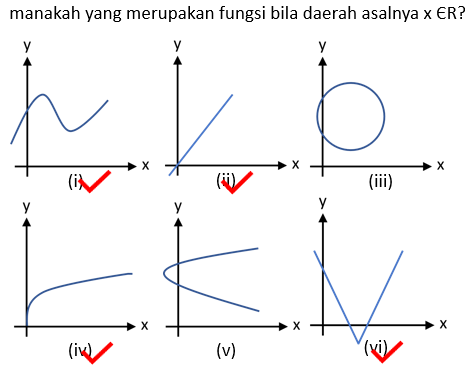
>> Diagram panah

>> Grafik fungsi

Grafik (iii) dan (v) bukanlah fungsi, karena ada x yang memiliki dua nilai y atau f(x) (x dipasangkan tepat satu anggota f(x)).
Sebuah fungsi dapat dinotasikan dengan huruf kecil seperti, f, g, h. Misalnya, fungsi g memetakan himpunan A ke himpunan B dinotasikan g(x) dengan aturan g: x ➝ x2 -2x. Ini berarti fungsi g memetakan x ke x2 -2x. Bayangan x oleh fungsi g adalah x2 -2x sehingga dapat dituliskan g(x) = x3 - 2x.
Contoh
Diketahui fungsi g: x ➝ x2 -2x pada himpunan bilangan real.
Tentukan:
a. g(2)
b. Bayangan (-3) oleh g
c. Nilai g untuk x = 1/2
d. Nilai x untuk g(x) = -1
e. Nilai p jika g(p) = 3
Pembahasan
a. g(x) = x2 - 2x
maka g(2) = 22 - 2(2) = 4 - 4 = 0
b. g(x) = x2 - 2x
maka g(-3) = (-3)2 - 2(-3) = 9+ 6 = 15
c. g(x) = x2 - 2x
maka g(1/2) = (1/2)2 - 2(1/2) = (1/4) + 1 = 5/4
d. g(x) = -1
⇒x2 - 2x = -1
⇔x2 - 2x +1= 0
⇔(x-1)(x-1)= 0
⇔(x-1)=0
⇔x = 1
e. g(p) = 3

b. Diketahui g(x) = x2 - 2x, maka g(-x) = (-x)2 - 2(-x) = x2 + 2x ≠ g(x) dan juga g(-x) ≠ -g(x), sehingga g bukanlah fungsi genap dan fungsi ganjil.
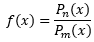 , dengan Pn(x) dan Pm(x) adalah polinom.
, dengan Pn(x) dan Pm(x) adalah polinom.
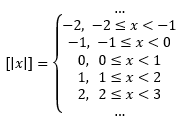
⇒x2 - 2x = 3
⇔x2 - 2x -3= 0
⇔(x+1)(x-3)= 0
⇔(x+1)=0 atau x-3=0
⇔x = -1 atau x =3
Unsur-unsur Pembentuk Fungsi
Variabel
Variabel adalah unsur yang sifatnya berubah-ubah dari satu keadaan ke keadaan lainnya. Simpelnya, variabel adalah lambang pengganti bilangan yang belum diketahui nilainya. Terdapat dua jenis variabel yang tedapat dalam fungsi, yaitu variabel bebas dan variabel terikat. Variabel bebas (independent) adalah variabel yang menjelaskan variabel lainnya, sedangkan variabel terikat (dependent) adalah variabel yang dijelaskan oleh variabel bebas, nilainya bergantung pada veariabel bebas.
Koefisien
Koefisien adalah faktor konstanta dari suatu variabel. Simpelnya, koefisien adalah bilangan yang terletak tepat di depan suatu variabel, terkait dengan variabel yang bersangkutan.
Koefisien adalah faktor konstanta dari suatu variabel. Simpelnya, koefisien adalah bilangan yang terletak tepat di depan suatu variabel, terkait dengan variabel yang bersangkutan.
Konstanta
Konstanta adalah suatu unsur yang sifatnya tetap dan tidak terkait dengan suatu variabel apapun.
Konstanta adalah suatu unsur yang sifatnya tetap dan tidak terkait dengan suatu variabel apapun.
Contoh
Misalkan terdapat fungsi f dengan f(x) = x2 - 2x + 4. Variabel bebas dalam f adalah x, dan variabel terikat dalam f adalah f(x) atau y. Satu adalah koevisien dari x2, -2 adalah koefisien dari x, dan 4 adalah konstanta.
Jenis-jenis Fungsi (Berdasarkan cara perpadanannya)
Misalkan A dan B adalah himpunan-himpunan yang tak kosong, dan fungsi f: A ⇾ B.
1. Fungsi Injektif / Fungsi Satu-satu
f dikatakan fungsi injektif, ditulis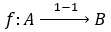 , apabila:
, apabila:
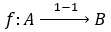 , apabila:
, apabila:(i) f(x1) = f(x2), maka x1 = x2
atau
(ii) x1 ≠ x2, maka f(x1) ≠ f(x2)
dengan x1, x2 ∈ A.

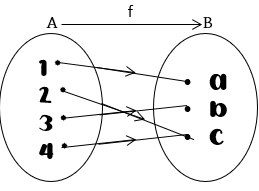
Intinya, f dikatakan fungsi injektif apabila setiap nilai fungsi atau f(x) (range) dipasangkan tepat satu anggota A (domain). Ih,{d} ga ada pasangannya kok dibilang fungsi injektif? Karena {d} adalah anggota dari kodomain, bukan range. Dengan kata lain, semua anggota Df (domain) memiliki pasangan tepat satu anggota B (kodomain), walaupun ada anggota B yang tidak memiliki pasangan.
2. Fungsi Surjektif / Onto (Pada)
f dikatakan fungsi surjektif, ditulis 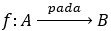 , apabila Rf = B (Daerah hasilnya adalah himpunan B). Dengan kata lain, untuk setiap y ∈ B, terdapat x ∈ A, sedemikian sehingga, f(x) = y.
, apabila Rf = B (Daerah hasilnya adalah himpunan B). Dengan kata lain, untuk setiap y ∈ B, terdapat x ∈ A, sedemikian sehingga, f(x) = y.
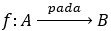 , apabila Rf = B (Daerah hasilnya adalah himpunan B). Dengan kata lain, untuk setiap y ∈ B, terdapat x ∈ A, sedemikian sehingga, f(x) = y.
, apabila Rf = B (Daerah hasilnya adalah himpunan B). Dengan kata lain, untuk setiap y ∈ B, terdapat x ∈ A, sedemikian sehingga, f(x) = y.
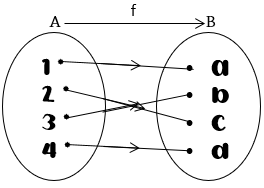
Jadi intinya, semua anggota B memiliki pasangan.
3. Fungsi Into
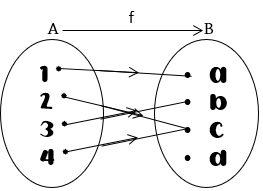
Jika f bukan fungsi surjektif, maka f dikatakan fungsi into dan ditulis 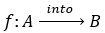 . Atau f dapat dikatakan fungsi into apabila terdapat anggota himpunan B yang tidak memiliki pasangan anggota himpunan A.
. Atau f dapat dikatakan fungsi into apabila terdapat anggota himpunan B yang tidak memiliki pasangan anggota himpunan A.
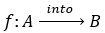 . Atau f dapat dikatakan fungsi into apabila terdapat anggota himpunan B yang tidak memiliki pasangan anggota himpunan A.
. Atau f dapat dikatakan fungsi into apabila terdapat anggota himpunan B yang tidak memiliki pasangan anggota himpunan A. 
4. Fungsi Bijektif/ Fungsi Satu-satu dan Pada
Jika fungsi f satu-satu dan pada, maka f dikatakan fungsi bijektif.

Contoh
Periksa manakah yang merupakan fungsi satu-satu dan fungsi onto.
a. f: R ⇾ R dengan f(x) = x3 - 1
b. g: R ⇾ R dengan g(x) = x2 - 2x
Pembahasan
a. Ambil x1, x2 ∈ Df dengan f(x1) = f(x2). Akan dibuktikan x1 = x2.
Karena f(x1) = f(x2), maka
x13 - 1 = x23 - 1 ⇔ x13 - x23 = 0
⇔ (x1 - x2)(x12 + x1x2 + x22) = 0
⇔ x1 - x2 = 0 atau x12 + x1x2 + x22= 0
⇔ x1 = x2 atau x1 = x2 = 0
Jadi terbukti f fungsi satu-satu.
Untuk setiap y ∈ R (kodomain), terdapat x = (y + 1)1/3 ∈ R (domain) sedemikian sehingga
g(x) = g((y+1)1/3) = ((y+1)1/3)3 - 1 = y + 1 - 1 = y.
Jadi terbukti f fungsi pada atau onto.
Karena f fungsi satu-satu dan onto, dapat dikatakan f fungsi bijektif.
 |
| Sumber: Geogebra.org |
Apabila ditinjau dari grafik fungsi nya, terlihat untuk setiap x ∈ R = Df dipasangkan tepat satu y ∈ R = Rf [fungsi satu-satu], serta setiap y memiliki pasangan x [fungsi onto].
b. Ambil -1 ∈ Dg dan 3 ∈ Dg. Jelas -1 ≠ 3. Akan tetapi, g(-1) = (-1)2 - 2(-1) = 3 = (3)2 - 2(3) = g(3). Ini berarti fungsi g bukan satu-satu.
Ambil -2 ∈ R = Rg. -2 = x2 - 2x ⇔ x2 - 2x + 2 = 0 di mana tidak ada nilai x yang memenuhi x2 - 2x + 2 = 0 sehingga -2 tidak memiliki pasangan di domain R. Dengan kata lain, terdapat y ∈ R = Rg yang tidak memiliki pasangan x ∈ R = Dg. Ini berarti fungsi g bukan onto.
 |
| Sumber: Geogebra.org |
Apabila ditinjau dari grafik fungsi nya, terlihat terdapat nilai y ∈ R = Rg yang berpasangan dengan dua nilai x ∈ R = Dg. Misalnya y = 0 yang berpasangan dengan x = 0 dan x = 2. Jadi fungsi g bukan satu-satu. Terlihat juga nilai y (y < -1) yang tidak memiliki pasangan padahal y adalah anggota kodomain. Jadi fungsi g juga bukan fungsi onto.
Jenis-jenis Fungsi (Berdasarkan Kesimentrian Grafik)
Terdapat dua jenis fungsi apabila dilihat dari kesimentrian grafiknya, yaitu fungsi genap dan fungsi ganjil. Fungsi genap memiliki grafik yang simetri terhadap sumbu y, sedangkan fungsi ganjil memiliki grafik yang simetri terhadap titik O (0,0). Untuk memperjelas, berikut definisinya.
Diberikan f fungsi sebarang.
f dikatakan fungsi genap apabila f(-x) = f(x) untuk setiap x ∈ Df.
f dikatakan fungsi ganjil apabila f(-x) = -f(x) untuk setiap x ∈ Df.
Contoh
Periksa apakah fungsi-fungsi berikut merupakan fungsi genap atau ganjil atau tidak keduanya.
a. f: R ⇾ R dengan f(x) = x3 - 1
b. g: R ⇾ R dengan g(x) = x2 - 2x
c. h: R ⇾ R dengan h(x) = x3 + x
d. s: R ⇾ R dengan s(x) = |x - 1|
e. f: R ⇾ R dengan f(x) = x
f. g: R ⇾ R dengan g(x) = x2+ 4
Pembahasan
a. Diketahui f(x) = x3 - 1, maka f(-x) = (-x)3 - 1 = -x3 - 1= -(x3 + 1) ≠ f(x) dan juga f(-x) ≠ -f(x), sehingga f bukanlah fungsi genap dan fungsi ganjil.
c. Diketahui h(x) = x3 + x, maka h(-x) = (-x)3 + (-x) = -x3 - x = -(x3 + x) = -h(x), sehingga h adalah fungsi ganjil.
d. Diketahui s(x) = |x - 1|, maka
s(x) = x - 1, jika x ≥ 1
s(x) = -x + 1, jika x < 1
sehingga
s(-x) = -x - 1, jika x ≤ -1
s(-x) = x + 1, jika x > 1
Jadi s(-x) ≠ s(x) dan juga s(-x) ≠ -s(x). Ini berarti fungsi s bukanlah fungsi ganjil maupun genap.
e. Diketahui f(x) = x, maka f(-x) = -x = -f(x), sehingga f adalah fungsi ganjil.
f. Diketahui g(x) = x2+ 4, maka g(-x) = (-x)2+ 4 = x2+ 4 = g(x), maka g adalah fungsi genap.
Jenis-jenis Fungsi (Berdasarkan Operasinya)
Apabila dilihat dari operasi yang bekerja pada fungsi, fungsi dibedakan menjadi dua yaitu, fungsi aljabar dan fungsi transenden.
Fungsi Aljabar
Fungsi aljabar adalah fungsi yang diperoleh melalui operasi aljabar (penjumlahan, pengurangan, perkalian, pembagian, dan penarikan akar). Fungsi aljabar terdiri dari:
a. Fungsi rasional
Bentuk umum:
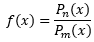 , dengan Pn(x) dan Pm(x) adalah polinom.
, dengan Pn(x) dan Pm(x) adalah polinom. Fungsi-fungsi yang termasuk fungsi rasional adalah fungsi linear, fungsi kuadrat, fungsi polinom, fungsi pecahan dkk.
b. Fungsi Irasional
Fungsi irasional adalah bentuk akar dari fungsi rasional.
Fungsi Transenden
adalah fungsi yang bukan fungsi aljabar, yaitu fungsi trigonometri, fungsi siklometri (invers dari trigonometri), fungsi eksponen, fungsi logaritma, dan fungsi hiperbolik.
Fungsi Khusus
1. Fungsi Konstan
Fungsi konstan adalah fungsi yang memetakan semua bilangan real ke konstanta. Misalkan terdapat fungsi f dengan aturan f(x) = c dengan c adalah konstanta. Contoh: g(x) = 4, h(x) = -5/2.
2. Fungsi Mutlak
Fungsi mutlak adalah fungsi yang variabel bebasnya terdapat dalam tanda mutlak.
3. Fungsi Tangga atau Fungsi Bilangan Bulat Terbesar
Bilangan bulat terbesar dari x ∈ R, dapat ditulis [|x|], didefinisikan sebagai bilangan bulat terbesar yang lebih kecil atau sama dengan x. Dengan kata lain [|x|] = k jika dan hanya jika k ≤ x ≤ k+1 dengan k adalah bilangan bulat.
Contoh
a. [|4,7|]
b. [|-8,2|]
c.[|100|]
Pembahasan:
a. Bilangan bulat terbesar yang kurang dari 4,7 adalah 4, sehingga [|4,7|] = 4.
b. Bilangan bulat terbesar yang kurang dari -8,2 adalah -9, sehingga [-8,2|] = -9.
c. Bilangan bulat terbesar yang kurang atau sama dengan 100 adalah 100, sehingga [|100|] = 100.
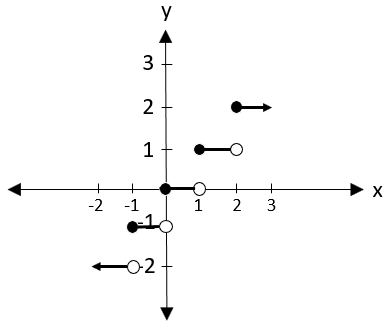
Fungsi bilangan bulat terbesar adalah fungsi yang memuat bentuk [| |]. Misalkan diketahui f(x) = [|x|], x ∈ R. Fungsi ini memiliki Df = R dan Rf = Z (himpunan bilangan bulat). Fungsi bilangan bulat terbesar dapat dinyatakan seperti berikut ini.
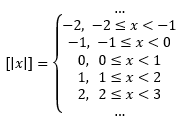
sketsa grafiknya

Karena bentuk grafik fungsinya seperti tangga, makanya dinamakan fungsi tangga.
--------------------------------------------------------------------------------------------------------------------------------------------------------------
Begitulah mengenai relasi dan fungsi. Selanjutnya akan dibahas mengenai operasi pada fungsi, fungsi komposisi, dan invers fungsi.
Semoga artikel ini dapat bermanfaat yaa. Silakan komen apabila ada yang keliru, agar kita belajar bersama.
Selamat belajar~
Salam Ngemeal 🍲
Sumber:
Dedy, E., dkk. (2005). Kalkulus I. Malang: Universitas Negeri Malang.




Komentar
Posting Komentar