Eksponen (Part II): Bentuk Akar Beserta Fungsi, Persamaan, dan Pertidaksamaannya Kelas 10
dengan a ∊ bilangan real, m ∊ bilangan bulat, n ∊ bilangan asli. Terlihat bahwa bilangan berpangkat pecahan tersebut dapat diubah menjadi bentuk akar. Dengan kata lain, bentuk akar adalah bentuk lain untuk menyatakan bilangan berpangkat.Bentuk akar termasuk ke dalam bilangan irasional, yaitu bilangan yang tidak bisa dinyatakan ke dalam bentuk a/b, dengan a,b ∈ bilangan bulat dan b ≠ 0. Misalnya √2, √3,√5, √6, √7, √11, √13, dan masih banyak lagi. Apabila terdapat bilangan yang bisa dinyatakan ke dalam bentuk a/b, dengan a,b ∈ bilangan bulat dan b ≠ 0, maka bilangan tersebut disebut bilangan rasional. "Tapi kan √2 bisa jadi √2/1, berarti √2 bilangan rasional?" Tentu saja bukan, karena √2 bukanlah bilangan bulat. "Kalau √9 pasti termasuk bilangan irasional, kan? soalnya ada tanda akarnya" Jawabannya √9 adalah bilangan rasional, karena √9 = 3 dan 3 bisa dinyatakan 3/1. Jadi hati-hati, tidak semua bilangan yang menggunakan tanda akar "√" merupakan bentuk akar.
Nilai √a ada jika a ≥ 0 (a bernilai positif) dan a ∊ bilangan real. Tidak ada akar dari bilangan negatif (√-2 tidak ada). Intinya, nilai di dalam tanda akar harus positif.
Sama halnya dengan bilangan berpangkat, bentuk akar juga memiliki sifat-sifat, diantaranya:
Operasi Aljabar pada Bentuk Akar
Penjumlahan dan Pengurangan
Jika a, b ∊ bilangan real dan c ≥ 0, maka:
(i) a√c + b√c = (a + b)√c
(ii) a√c - b√c = (a - b)√c
Contoh
1). 12√3 + 7√3 = (12+7)√3 = 19√3
2). 4√20 - 6√5 + 2√7 = 4√(4x5) - 6√5 + 2√7
= 4√4 √5 - 6√5 + 2√7
= 4(2) √5 - 6√5 + 2√7
= 8√5 - 6√5 + 2√7
= (8-6)√5 + 2√7
= 2√5 + 2√7
Perkalian
Jika a, b ∊ bilangan real dan c, d ≥ 0, maka a√c x b√d = ab√(cd)
Contoh
1). 2√3 x 4√12 = (2x4)√(3x12)
= 8√36
= 8 (6)
= 48
2). 6√72 x 5√74 = (6x5)√72+4
= 30 √76
= 30 (76)1/2
= 30 (73)
= 30 (343)
= 10290
Pembagian
Jika a, b ∊ bilangan real, b ≠ 0, c ≥ 0, dan d > 0, maka
Contoh
1) 2√6 : 3√2 = (2/3) x √(6/3) = (2/3) √2
2) 28√59 : 7√57 = (28/7) x √(59-7) = 4 √52 = 4 (5) = 20
Merasionalkan Bentuk Akar
Untuk memudahkan dalam menyelesaikan persoalan bentuk akar, ada baiknya bentuk akar dituliskan dalam bentuk yang paling sederhana (rasional). Berikut ciri-ciri bentuk akar yang perlu dirasionalkan.
(i) Memuat faktor yang pangkatnya lebih dari satu
Contoh:
√x9, agar sederhana dapat diubah menjadi √x8+1 = √x8.x = x4√x
(ii) Mengandung pecahan
Contoh:
√(3/8), agar sederhana dapat diubah menjadi (√3/√8) x (√8/√8) = (√24)/8 = (2√6)/8 = (√6)/4
(iii) Bentuk akar sebagai penyebut
Merasionalkan penyebut pecahan bentuk akar berarti mengubah penyebut yang berbentuk akar menjadi bentuk rasional (tidak ada akar). Untuk merasionalkannya, pembilang dan penyebut pecahan tersebut dikalikan dengan bentuk akar yang sekawan dengan penyebutnya,
Intinya, sekawannya positif (+) adalah negatif (-), begitu pula sebaliknya.
Ingat!!!
(a + b)(a - b) = a2 - b2
Contoh
Bentuk Akar dalam Akar
Untuk a, b ∈ bilangan rasional positif dan a > b > 0, berlaku:
(i) (√a + √b)2 = (a + b) + 2√(ab)
atau
(ii) (√a - √b)2 = (a + b) - 2√(ab)
atau
Contoh
Persamaan dan Pertidaksamaan Bentuk Akar
Masih ingat bedanya persamaan dan pertidaksamaan, kan? Persamaan dihubungankan dengan tanda sama dengan "=", sedangkan pertidaksamaan dihubungkan dengan tanda selain sama dengan, yaitu "≠", "≥", "≤", ">", dan "<".
Persamaan dan pertidaksamaan bentuk akar (irasional) adalah persamaan dan pertidaksamaan yang variabelnya terdapat dalam tanda akar.
Contoh:
(i) √(x+1) = 2 [persamaan bentuk akar]
(ii) √(a2 - 5a + 6) > 3 [pertidaksamaan bentuk akar]
(iii) x√3 - √5 = √15 [bukan persamaan bentuk akar]
(iv) (3a - √3)(a√3 + √2) < 9 [bukan pertidaksamaan bentuk akar]
Bentuk umum persamaan bentuk akar:
(i) √f(x) = a dengan f(x) ≥ 0 dan a adalah bilangan real positif atau nol
(ii)√f(x) = g(x) dengan f(x) ≥ 0
(iii) √f(x) = √g(x) dengan f(x) ≥ 0 dan g(x) ≥ 0
Bentuk umum pertidaksamaan bentuk akar:
(i) √f(x) * a dengan f(x) ≥ 0
(ii)√f(x) * g(x) dengan f(x) ≥ 0
(iii) √f(x) * √g(x) dengan f(x) ≥ 0 dan g(x) ≥ 0
Tanda * bisa diganti "≥", "≤", ">", atau "<" (keliatan banget males ngetik hehe).
Terdapat persamaan dan pertidaksamaan bentuk akar yang sudah pasti tidak memiliki penyelesaian, yaitu:
1). √f(x) = a dengan a < 0 (karena hasil akar tidak pernah negatif)
2). √f(x) < a dengan a < 0 (karena hasil akar tidak pernah negatif)
3). √f(x) ≤ a dengan a < 0 (karena hasil akar tidak pernah negatif)
Menyelesaikan persamaan atau pertidaksamaan artinya kita harus mencari nilai pengganti variabel yang memenuhi persamaan ataupun pertidaksamaan tersebut. Untuk menyelesaikan persamaan bentuk akar (akar pangkat dua), tinggal kuadratkan saja kedua ruasnya, lalu akan didapat penyelesaiannya. Jika bentuk akarnya akar pangkat n, maka kedua ruas dipangkatkan n. Sedangkan untuk menyelesaikan pertidaksamaan bentuk akar, terdapat beberapa langkah.
Langkah 1:
Tentukan syarat untuk bilangan dalam akar dan akan didapatkan himpunan penyelesaian pertama. Ingat!! Bilangan di dalam akar adalah bilangan real positif atau nol (√f(x) ada jika f(x) ≥ 0).
Langkah 2:
Jika bentuk akarnya akar pangkat dua (√), kuadratkan kedua ruas dan selesaikan hingga didapatkan himpunan penyelesaian kedua. Tanda pertidaksamaan tidak berubah. Jika bentuk akarnya akar pangkat n, maka kedua ruas dipangkatkan n. Tapi biasanya untuk soal tingkat SMA, bentuk akarnya akar pangkat dua.
Langkah 3:
Himpunan penyelesaian dari pertidaksamaan adalah irisan dari himpunan penyelesaian langkah 1 dan himpunan penyelesaian langkah 2.
Contoh
Tentukan himpunan penyelesaian dari:
1). √(x + 7) < 3
2). √(5x - 4) = √(2x + 1)
3). √(x-1) - 2√x ≥ 0
4). √(x2 - 16) = √(x + 4)
5). 3√(x-3) > 4
6. √(x2 - 5x + 6) = -11
Pembahasan:
1). √(x + 7) < 3
» x + 7 ≥ 0
⇔ x ≥ -7
» (√(x + 7))2 < 32
⇔ x + 7 < 9
⇔ x < 2
» Irisan dari x ≥ -7 dan x < 2 adalah -7 ≤ x < 2
Jadi, HP = {x | -7 ≤ x < 2}
2). √(5x - 4) = √(2x + 1)
(√(5x - 4))2 = (√(2x + 1))2
⇔ 5x - 4 = 2x + 1
⇔ 3x = 5
⇔ x = 5/3
Jadi, HP = {5/3}
3). √(x-1) - 2√x ≥ 0
⇔ √(x-1) ≥ 2√x
» x - 1 ≥ 0
⇔ x ≥ 1
x ≥ 0
» (√(x - 1))2 ≥ (2√x)2
⇔ x - 1 ≥ 4x
⇔ -3x ≥ 1
⇔ x ≤ -1/3
» Irisan dari x ≥ 1, x ≥ 0, dan x ≤ -1/3 adalah Ø atau { }.
Jadi HP = { }.
4). √(x2 - 16) = √(x + 4)
(√(x2 - 16))2 = (√(x + 4))2
⇔ x2 - 16 = x + 4
⇔ x2 - 16 -x - 4 = 0
⇔ x2 - x - 20 = 0
⇔ (x - 5)(x + 4) = 0
⇔ x - 5 = 0 atau x + 4 = 0
⇔ x = 5 atau x = -4
Jadi, HP = {-4, 5}
5). 3√(x-3) > 4
» x - 3 ≥ 0
⇔ x ≥ 3
» (3√(x - 3))3 > 33
⇔ x - 3 > 27
⇔ x > 24
» Irisan dari x ≥ 3 dan x > 24 adalah x>24
Jadi, HP = {x | x > 24}
6). √(x2 - 5x + 6) = -11
Tidak memiliki penyelesaian, kerena hasil akar tidak ada yang negatif.
Fungsi Bentuk Akar atau Fungsi Irasional
Fungsi irasional adalah bentuk akar dari fungsi rasional, yaitu fungsi yang berbentuk umum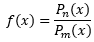 
, dengan Pn(x) dan Pm(x) adalah polinom. Atau pengertian simpelnya, fungsi yang variabel bebasnya terdapat di dalam akar.
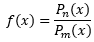, dengan Pn(x) dan Pm(x) adalah polinom. Atau pengertian simpelnya, fungsi yang variabel bebasnya terdapat di dalam akar. Bentuk Umum:
dengan Pn(x)/Pm(x) ≥ 0.
Daerah asal fungsi irasional bergantung pada nilai dalam akarnya. Syarat bentuk akar adalah nilai dalam akar haruslah bernilai positif atau nol. Fungsi irasional juga begitu. Fungsi irasional akan terdefinisi bila nilai dalam akar bernilai positif atau nol sehingga daerah asal dapar ditentukan dari syarat tersebut.
Nilai akar tidak pernah negatif, sehingga daerah hasil (range) dari fungsi irasional adalah semua bilangan real positif y atau nol, ditulis Rf = {y| y ≥ 0} atau Rf = y ∈ [0, ∞).
Contoh
g(x) = √x
Syarat fungsi g terdefinisi adalah nilai dalam akar haruslah positif atau nol, atau x ≥ 0. Sehingga daerah asl (domain)nya adalah semua bilangan x lebih dari atau sama dengan nol, ditulis Dg = {x| x ≥ 0} atau Dg = x ∈ [0, ∞). Daerah hasil (range) nya adalah semua bilangan real positif y atau nol, ditulis Rg = {y| y ≥ 0} atau Rg = y ∈ [0, ∞).
Menggambar grafik fungsi irasional tidak berbeda dengan grafik fungsi lain. Apabila kita mengetahui daerah asal fungsinya, menggambar grafik akan jauh lebih mudah. Diketahui domain fungsi g adalah x ≥ 0. Ambil sebarang x yang lebih dari atau sama dengan nol. Misalnya 0, 1, 4, 9. Dari sebarang x tersebut, kita cari nilai fungsinya sehingga diperoleh titik koordinat.
g(0) = √0 = 0 ⇒ (0,0)
g(1) = √1 = 1 ⇒ (1,1)
g(4) = √4 = 2 ⇒ (4,2)
g(9) = √9 = 3 ⇒ (9,3)
Tinggal letakkan titik-titik koordinat pada bidang Cartesius. Lalu hubungkan titik-titik koordinat yang diperoleh sehingga membentuk kurva mulus. Jadi deh grafiknya.
 |
| sumber: geogebra.org |
Nah, agar lebih jago lagi, ayo kita latihan soal!
1). Tentukan bentuk sederhana dari:
a. (1 + 3√2) - (4 - √50)
b. (3√2 - 2√3)(2√3 + √2)
2). Tentukan nilai a + b, jika a dan b ∈ bilangan positif.
3).
Silakan coba dikerjakan sendiri terlebih dahulu yaa...
----------------------------------------------------------------------------------------------------------------------------------------------
Pembahasan:
1). a. (1 + 3√2) - (4 - √50) = 1 + 3√2 - 4 + √50
= -3 + 3√2 + √(25x2)
= -3 + 3√2 + √(25x2)
= -3 + 3√2 + 5√2
= -3 + 8√2
= -3 + 8√2
b. (3√2 - 2√3)(2√3 + √2) = (3√2)(2√3) + (3√2)(√2) + (-2√3)(2√3) + (-2√3)(√2)
= 6√6 + 6 - 12 - 2√6
= - 6 + 4√6
2).
3).
Itulah penjelasan mengenai eksponen bentuk akar. Jangan lupa terus berlatih agar lebih mantaps lagi pemahamannya. Untuk selanjutnya akan dibahas mengenai persamaan dan pertidaksamaan bilangan berpangkat.
Semoga artikel ini bermanfaat. Apabila ada yang keliru, silakan komen yaa..
Selamat belajar~
Salam ngemeal 🍲
Komentar
Posting Komentar