Eksponen (Part I): Definisi, Sifat, Grafik Fungsi Beserta Contoh Kelas 10

Tau gak sih kalau "2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2" dapat ditulis lebih ringkas? Pasti tau doong. Perkalian tersebut dapat dituliskan sebagai bilangan berpangkat atau bilangan eksponen, yaitu 2¹⁶ , karena 2 dikalikan dirinya sendiri sebanyak 16 kali. Jadi, sebenarnya eksponen itu nama lain dari pangkat. Untuk lebih jelasnya, berikut definisi dari eksponen.

Definisi Eksponen

Untuk setiap a ∊ bilangan real dan n ∊ bilangan asli, notasi aⁿ adalah hasil kali n buah faktor a, atau dapat dituliskan

                                                

dengan a adalah bilangan pokok atau basis

            n adalah eksponen atau pangkat atau indeks

aⁿ dibaca "a pangkat n" atau "a eksponen n".

Contoh: (i) 5⁶ = 5 x 5 x 5 x 5 x 5 x 5

              

              (iii) (-3)⁴ = (-3) x (-3) x (-3) x (-3)

Terdapat pula beberapa bentuk bilangan berpangkat, yaitu:

a. Pangkat Nol (a⁰)

    a⁰ = 1 dengan a ∊ bilangan real dan a ≠ 0.

    Contoh: 10⁰ = 1, (1/2)⁰ = 1, (-1200)⁰ = 1 

b. Pangkat Negatif (a^-n)

     dengan a ∊ bilangan real, a ≠ 0, n ∊ bilangan asli, dan n ≠ 0. 

    Akibatnya,  dengan syarat yang sama.
    Contoh:

                 

c. Pangkat Pecahan (a^m/n)

     dengan a ∊ bilangan real, m ∊ bilangan bulat, n ∊ bilangan asli.

    Contoh: 

                

Sifat-Sifat Eksponen

Dari definisi eksponen, diperoleh sifat-sifat eksponen, diantaranya:

(i) a^m. aⁿ = a^m+n

(ii) , dengan a ≠ 0

(iii) (a^m)ⁿ = a^mn

(iv) (ab)ⁿ = aⁿ. bⁿ

^(v) , dengan b ≠ 0

(vi) , dengan a > 0

(vii) Jika a, m, n ∊ bilangan real dan a > 0, a^m = aⁿ, maka m = n

Contoh 1

Hitunglah: a). (-2³)² 

                  b).

                  c). 

Pembahasan:

a). (-2³)² 

     Dengan menggunakan sifat (iii), diperoleh:

     ((-2)³)² = (-2)^3x2 = (-2)⁶ = 64

b). 

c).

        

Contoh 2

Sederhanakanlah: a). (4x³y^-2)³(2y⁹z)²

                             b). 
                             c). 

Pembahasan:

a). (4x³y^-2)³(2y⁹z)² = (4³x^3x3y^-2x3)(2²y^9x2z²)

                                = (4³x⁹y^-6)(4y¹⁸z²)

                                = 4³⁺¹ x⁹ y^-6+18 z²
                                = 4⁴ x⁹ y¹² z²
                                = 256x⁹y¹²z²

b). 

    

c. 

    

Fungsi Eksponen

Bentuk Umum: f(x) = a^x

                         dengan a > 0, a ≠ 1, x ∈ bilangan real

Daerah asal (domain) dari fungsi eksponen tersebut adalah semua bilangan real atau dapat dituliskan D_f = {x| x ∈ R}, sedangkan daerah hasil (range) adalah semua bilangan real positif atau dapat dituliskan R_f = {f(x) = y | y > 0, y ∈ R}. 

Contoh:

(i) y = f(x) = 4^x (fungsi eksponen)

(ii) y = f(x) = 3,7^x (fungsi eksponen)

(iii) y = f(x) = (1/2)^x(fungsi eksponen)

(iv) y = f(x) = 1^x (bukan fungsi eksponen)

(v) y = f(x) = x³ (bukan fungsi eksponen)

Terdapat bentuk fungsi eksponen yang lebih kompleks. Maka dari itu, memiliki daerah hasil (range) yang berbeda pula, tergantung bentuk fungsi eksponennya.

f(x) = k . a^g(x) + b

dengan a sebagai basis di mana a > 0, a ≠ 1

            b, k ∈ bilangan real sebagai konstanta

            g(x) sebagai pangkat atau eksponen

Contoh: 

(i) f(x) = 3. 4^x

(ii) f(x) = 4^x - 3

(iii) f(x) = 4^{x^2 +4x +4} + 5

(iv) f(x) = 7. 2^{x -1} - 6

Contoh 3

Tentukan nilai fungsi untuk x = 3

a. f(x) = 3^x

b. f(x) = 2^-x

c. f(x) = (1/4)^x

d. f(x) = 3^{x -2}

Pembahasan:

a. f(x) = 3^x

    f(3) = 3³ = 27     

b. f(x) = 2^-x 

    f(3) = 2^-3 = 1/(2³) = 1/8

c. f(x) = (1/4)^x

    f(3) = (1/4)³ = 1³/4³ = 1/64

d. f(x) = 3^{x -2}   

    f(3) = 3^{3 -2} = 3¹ = 3

Contoh 4

Misalkan seorang peneli melakukan pengamatan terhadap bakteri A. Setiap hari bakteri membelah diri menjadi dua. Pada awal pengamatan terdapat 3 bakteri. Berapa banyak bateri A  dua minggu kemudian? 

Pembahasan:

Hari 0    : 3 bakteri

Hari 1    : 3 x 2 = 3 x 2¹ = 6 bakteri

Hari 2    : 6 x 2 = 3 x 2² = 12 bakteri

Hari 3    : 12 x 2 = 3 x 2³ = 24 bakteri

maka

Hari n    : 3 x 2ⁿ bakteri

Dua minggu = 14 hari

sehingga di hari ke 14, akan ada 3 x 2¹⁴ atau 49152 bakteri.

Grafik Fungsi Eksponen

Fungsi eksponen sering kali digunakan dalam kehidupan sehari-hari. Biasanya digunakan dalam hal yang berkaitan dengan pertumbuhan dan peluruhan. Pasti kalian tidak asing dengan virus corona, bukan? Kasus corona di Indonesia masih terus bertambah. Perhatikan grafik berikut ini.

sumber: kumparan.com

Inilah salah satu contoh grafik fungsi eksponen dan tentu saja ini bukanlah kabar baik. Tetap terapkan protokol kesehatan ya gaes. Jangan anggap sepele. Semoga pandemi ini cepat berakhir 😔.

Oke kembali ke topik.

Kita telah mengetahui bahwa fungsi eksponen adalah fungsi yang variabel (bebas) nya merupakan pangkat dari suatu bilangan, atau dapat kita tulis

y = f(x) = a^x  , dengan a > 0 dan a ≠ 1.

Dari a > 0 dan a ≠ 1, dapat pula ditulis menjadi 0 < a < 1 atau a > 1, sehingga kita dapat membagi grafik fungsi eksponen menjadi 2 kategori, yaitu:

(i) y = f(x) = a^x dengan 0 < a < 1

(ii) y = f(x) = a^x dengan a > 1

y = f(x) = a^x dengan 0 < a < 1

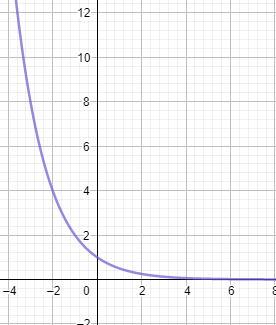
Dengan 0 < a < 1 (a berupa pecahan satuan), apabila x semakin besar maka nilai y semakin kecil, dan apabila x semakin kecil maka nilai y semakin besar. 

Contoh: f(x) = (1/2)^x

             

    

            

Sumber: geogebra.org

Terdapat karakteristik fungsi a^x dengan 0 < a < 1, yaitu:

(i) memotong sumbu y di titik (0,1)

(ii) fungsi turun (monoton turun) karena semakin besar x maka semakin kecil y.

(iii) kurva berada di atas sumbu x (karena nilai y selalu positif)

(iv) sumbu x sebagai asimtot datar (a^x➝ 0 ⇒ x ➝ ∞)

(v) memiliki invers

y = f(x) = a^x dengan a > 1

Dengan a > 1 , apabila x semakin besar maka nilai y semakin besar pula, dan apabila x semakin kecil maka nilai y juga semakin kecil. 

Contoh: f(x) = 2^x

               

   

             

Sumber: geogebra.org

Terdapat karakteristik fungsi a^x dengan a > 1, yaitu:

(i) memotong sumbu y di titik (0,1)

(ii) fungsi naik (monoton naik) karena semakin besar x maka semakin besar y.

(iii) kurva berada di atas sumbu x (karena nilai y selalu positif)

(iv) sumbu x sebagai asimtot datar (a^x➝ 0 ⇒ x ➝ -∞)

(v) memiliki invers

Untuk menentukan asimtot datar fungsi eksponen, ada cara mudahnya.

(i) Jika fungsi eksponen berbentuk f(x) = a^x, maka asimtot datarnya adalah y = 0.

(ii) Jika fungsi eksponen berbentuk f(x) = a^x + b, maka asimtot datarnya adalah y = b.

Contoh 5

Gambarlah grafik f (x) = 3^x dengan x ∈ R.

Pembahasan:

(1) Menentukan titik-titik pada grafik

    

    Titik potong terhadap sumbu y (x = 0):

        f (0) = 3⁰ = 1

        Jadi, memotong sumbu y di titik (0,1)

    Tidak memotong sumbu x, karena y > 0

(2) Menentukan asimtot 

Asimtot suatu garis lengkung adalah garis lurus yang didekati garis lengkung sapai titik tak hingga dengan jarak semakin jauh semakin mendekati nol. Untuk bentuk f(x) = a^x asimtotnya adalah sumbu x atau y = 0. 

(3) Menentukan daerah asal dan daerah hasil

Karena 3^x terdeteksi untuk setiap x anggota bilangan real, maka daerah asal (domain) nya adalah himpunan bilangan real atau D_f = {x| x ∈ R}. Karena 3^x tidak pernah nol atau negatif, maka daerah hasil (range) nya adalah himpunan bilangan real positif atau R_f = {f(x) = y | y > 0, y ∈ R}.

Sumber: geogebra.org

Contoh 6

Gambarkan grafik f(x) = 2^x - 1 dengan x ∈ R.

Pembahasan:

(1) Menentukan titik-titik pada grafik

    

    Titik potong terhadap sumbu y (x = 0):

        f (0) = 2⁰ - 1 = 1-1 = 0

        Jadi, memotong sumbu y di titik (0,0)

    Titik potong terhadap sumbu x (y = 0):

         0 = 2^x - 1 ⇔ 2^x = 1 ⇔ x = 0

        Jadi, memotong sumbu x di titik (0,0)

(2) Menentukan asimtot 

      y = 2^x - 1

      Asimtot dicapai ketika a^x = 0, sehingga

      y = 0 -1 ⇔ y = -1

(3) Menentukan daerah asal dan daerah hasil

Karena 2^x - 1 terdeteksi untuk setiap x anggota bilangan real, maka daerah asal (domain) nya adalah himpunan bilangan real atau D_f = {x| x ∈ R}. Karena asimtot y = -1, maka daerah hasil (range) nya adalah himpunan bilangan real lebih dari -1 atau R_f = {f(x) = y | y > -1, y ∈ R}.

Sumber: geogebra.org

Contoh 7

Gambarkan grafik f(x) = -(1/3)^x dengan x ∈ R.

Pembahasan:

(1) Menentukan titik-titik pada grafik

    

    Titik potong terhadap sumbu y (x = 0):

        f (0) = -(1/3)⁰  = -1 

        Jadi, memotong sumbu y di titik (0,-1)

    Tidak memotong sumbu x.

(2) Menentukan asimtot 

      y = -(1/3)^x

      Asimtot dicapai ketika a^x = 0, sehingga

      y = - 0 = 0

(3) Menentukan daerah asal dan daerah hasil

Karena -(1/3)^x terdeteksi untuk setiap x anggota bilangan real, maka daerah asal (domain) nya adalah himpunan bilangan real atau D_f = {x| x ∈ R}. Karena -(1/3)^x tidak pernah nol atau positif, maka daerah hasil (range) nya adalah himpunan bilangan real negatif atau R_f = {f(x) = y | y < 0, y ∈ R}.

Sumber: geogebra.org

Kira-kira begitulah mengenai eksponen. Selanjutnya akan dibahas mengenai eksponen bentuk akar dan persamaan dan pertidaksamaan eksponen. 

Semoga bermanfaat ya. Komen ya apabila ada yang keliru atau mau memberikan saran.

Selamat belajar~

Salam ngemeal 🍲

Sumber: 

(i) https://www.geogebra.org/calculator

(ii) http://file.upi.edu/Direktori/FPMIPA/JUR._PEND._MATEMATIKA/195509091980021-KARSO/Modul_7_S1_PGSD.pdf

(iii) https://kumparan.com/makhyan-jibril/bom-waktu-itu-bernama-coronavirus-apa-yang-kita-dan-pemerintah-harus-lakukan-1t1V0EUHncs